Sommaire
2. Analyse théorique : présentation du problème
2.1 Une question difficile facilement écartée
2.2 Le cycle des crises au cœur de la prévision
2.3 A la recherche d’une des bases matérielles du cycle des crises.
3. La divergence entre la masse et la valeur du capital fixe
3.1 La reproduction du capital fixe
4.1 L’évolution de la part de la reproduction simple : exemple numérique
4.3 Le maximum du rapport entre taux d’accumulation et la période de rotation du capital fixe
5. L'élément cyclique de la reproduction simple
6. Evolution de l’accumulation de capital fixe
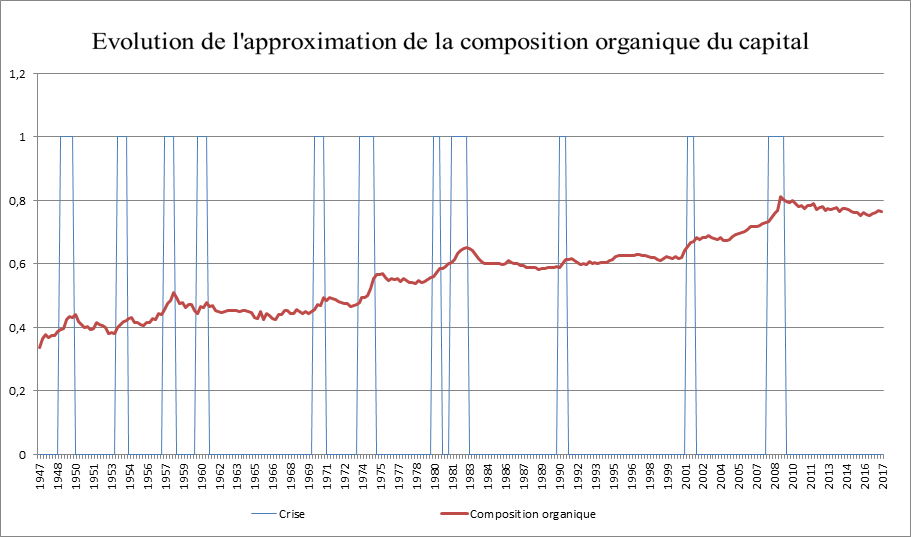
7. Evolution d’une approximation de la composition organique du capital
1. Introduction
Ce texte reprend en édition séparée, les chapitres 22 à 27 du livre consacré au cycle des crises aux Etats-Unis depuis 1929. Ces chapitres traitent du cycle du capital fixe. Ils démontrent mathématiquement que la reproduction du capital fixe et les variations dans l’accumulation de celui-ci induisent une onde dont la période est égale à la période de rotation du capital fixe.
Cette démonstration donne donc une base solide aux anticipations de Marx quant à l’incidence des variations de l’accumulation du capital fixe sur le cycle[1]. Ces variations sont permanentes, mais c’est à l’occasion des crises que l’on constate les plus importantes. En démontrant que la reproduction du capital fixe contient un élément cyclique et que la durée de ce cycle correspond à la période de rotation du capital fixe, nous donnons une assise aux perspectives de Marx quant aux relations entre cycle et reproduction du capital fixe.
Ce serait cependant une erreur[2] que de faire de cette reproduction du capital fixe, un facteur prépondérant du cycle alors qu’il n’en est, comme le remarque Marx, qu’un élément, une des bases matérielles. On peut même penser à l’issue de cette démonstration qu’elle joue un rôle autonome. En affectant le cycle à l’issue de la période de rotation du capital fixe, la forte variation précédente peut contribuer à précipiter ou accentuer la crise si les autres facteurs résultant du cycle de l’accumulation, du cycle financier, … sont mûrs pour que la crise éclate, sinon, si le cycle dépasse ou au contraire est plus court que la période de rotation du capital fixe, l’onde induite par les variations de l’accumulation y jouera un rôle de même nature mais d’une incidence plus faible.
Nous ne savons que peu de choses sur la période de rotation du capital fixe à l’époque actuelle. Quelle est sa durée ? A-t-elle une relative fixité ? A-t-elle tendance à se raccourcir ?
Comme nous l’expliquons dans le livre, au chapitre 7, sur le cycle des crises aux Etats-Unis, nous n’avons pas été à même de mettre en évidence dans les statistiques les effets du cycle du capital fixe[3]. En effet, nous n’avons pas trouvé de méthode permettant de relever dans les statistiques ce que la démonstration annonce. Peut-être que des camarades plus savants que nous y parviendront. C’est notamment à cet effet que nous publions ce texte sous une forme séparée de l’ouvrage qui le contient.
2. Analyse théorique : présentation du problème
2.1 Une question difficile facilement écartée
« De nombreux auteurs essaient de défendre cette politique (baisse artificielle des taux d'intérêt par l'expansion du crédit NDR) en produisant des explications fallacieuses du cycle économique et en passant sous silence la théorie monétaire. D'après eux, le retour des crises économiques est inscrit dans la nature même de l'économie libre de marché.
Le créateur de ce sophisme est Karl Marx. L'un des principaux dogmes de ses enseignements est que le retour périodique des crises commerciales est un trait caractéristique inhérent à « l'anarchie de la production » du capitalisme. Marx fit plusieurs pauvres tentatives contradictoires pour démontrer son dogme ; même les auteurs marxistes admettent que ces entreprises étaient totalement futiles. » (Ludwig von Mises, The Freeman, 24 septembre 1951, compte-rendu du livre de Alvin Hansen : Business Cycles and National Income, traduction sur le site d’Hervé de Quengo, http://herve.dequengo .free.fr)
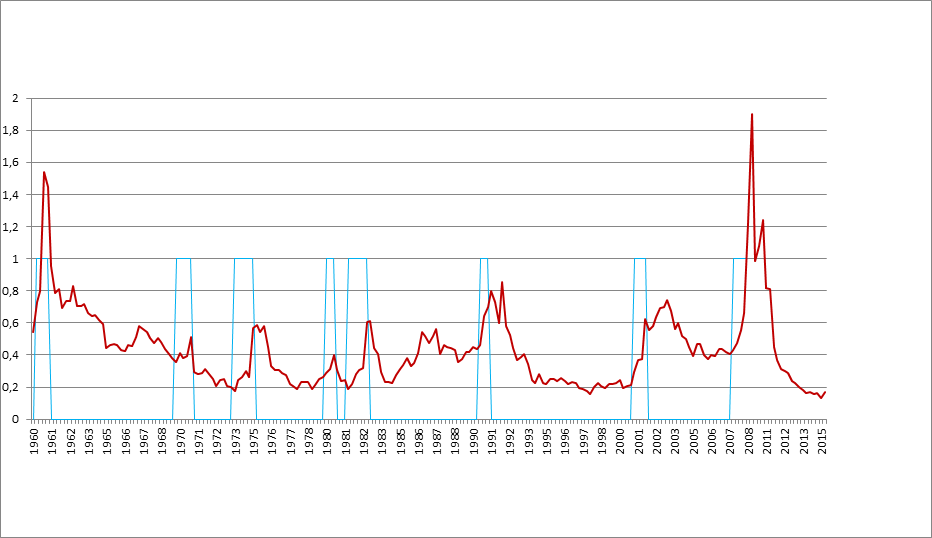
Voici comment s’exprimait, en 1951, un des défenseurs acharné du libéralisme. Evidemment, aujourd’hui, après tant de crises et notamment celle de 2008-2009, on ne peut avoir qu’un sourire de pitié devant tant de fanatisme imbécile, tandis que la théorie de Marx remporte une nouvelle et éclatante victoire.
Une théorie sur les origines du cycle ne va pourtant pas de soi et la gauche d’Italie, à la même époque où Ludwig von Mises vomissait ses injures, pouvait ainsi affirmer ironiquement que :
« Les difficiles problèmes du cadre et du cycle économiques, sur lesquels se cassèrent la tête ces petits collégiens de Quesnay, de Sismondi ou de Marx, deviennent un jeu d'enfants. La clé c'est le client, maître de la richesse; de même que le citoyen est le maître du pouvoir. Peu importe qu'il soit un simple travailleur salarié, un petit employé touchant traitement ou un petit-bourgeois; comme Charles-Quint le criait aux paysans d'Alghero : estate todos caballeros![4], le grand capital étasunien crie aux habitants de la terre entière : estate todos clientes![5] titre suprême de noblesse de l'économie mercantile. » (Le prolétariat comme client : la vulgarité de la politique économique des USA, Battaglia Comunista, no. 1, 1952)
Cette difficulté intrinsèque propre à la question du cycle, ainsi que l’inachèvement, on le verra, de la réflexion de Marx sur ce sujet ont poussé certains marxistes à écarter péremptoirement toute tentative d’approfondir la question quitte à falsifier le point de vue de Marx lui-même. Un représentant typique de cette façon de voir est Paul Mattick qui, dans son livre sur Marx et Keynes, affirme :
« Le cycle déterminé de crises, que le siècle dernier a traversé, constitue cependant un donné empirique dont la théorie marxienne n'a pas traité directement. Certes, Marx devait s'efforcer de rattacher cette périodicité fixe à la rotation du capital. Mais il n'insista guère cependant sur la validité de cette interprétation, et, de toute façon, sa théorie ne prend pas pour base une périodicité particulière des crises. Elle se borne à dire en effet que des crises éclatent forcément, sous forme de surproduction de capital et comme instrument pour assurer la reprise de l'accumulation » (Paul Mattick, Marx et Keynes, Gallimard, p.93)
2.2 Le cycle des crises au cœur de la prévision
Pourtant, n’en déplaise à la pensée bourgeoise et révisionniste, l’analyse des cycles comme de leur périodicité est au centre de la perspective révolutionnaire du marxisme. Dès l’origine, dès sa conception embryonnaire pourrait-on dire[6], de la conception matérialiste de l’histoire, cette étude du cycle est au cœur de la prévision quant au cours catastrophique du mode de production capitaliste et de l’action révolutionnaire qui peut en découler.
Engels, dès 1845, dans son ouvrage sur les classes laborieuses en Angleterre, prévoit deux nouvelles crises qui devraient se traduire par la victoire du prolétariat[7]. Seule la première prévision sera couronnée de succès et le mouvement révolutionnaire qui atteindra son apogée en 1848 sera brisé. Ce sera la contre révolution et non la révolution qui en sortira victorieuse. Les fondateurs du socialisme scientifique s'intéressèrent donc, dès sa gestation, au cycle des crises. De telles considérations avaient pour eux un caractère pratique immédiat. L'échec de la révolution de 1848, sa défaite pays par pays, conduit Marx à penser que la contre-révolution est nécessaire pour débarrasser le prolétariat de ses dernières illusions et le préparer à une nouvelle vague révolutionnaire. Celle-ci ne devrait pas manquer de se produire environ cinq ans après la crise de 1847, à l'occasion d'une nouvelle crise économique qui ébranlerait la production capitaliste. Marx et Engels tablaient donc, au début de 1850, sur un cycle des crises d'environ cinq ans. Cette analyse ne s'appuyait vraisemblablement pas encore sur de solides conceptions théoriques, mais sur la reconduction de constatations empiriques qui faisaient apparaître l'existence de crises, tous les cinq ans environ, depuis 1825. Ils se rendirent vite compte que cette perspective était erronée. Les faits devaient infirmer la prévision de Marx et Engels tandis que les crises s'espaçaient. Le cycle dont Marx était le témoin durait désormais environ dix ans. Marx ne renonça pas pour autant, bien au contraire, à l’idée que les crises étaient périodiques. Toute sa vie, il cherchera à en découvrir les racines et à en prévoir le retour, y compris par des méthodes mathématiques. Marx et Engels tireront de cet épisode l’idée qu’il existe, au sein du cycle des crises générales; des crises intermédiaires qui, si elles sont suffisamment fortes, peuvent escompter la crise générale[8]. Plus tard, Engels considérera que ces crises intermédiaires ont disparu[9]. Cependant, nous avons vu, notamment avec le cas des cycles à vagues, que d’une part, l’idée que les crises intermédiaires, quand elles existent, peuvent escompter la crise générale est toujours d’actualité (le cas du huitième cycle est particulièrement probant) et d’autre part, que des crises intermédiaires sont une composante de la tendance à la stagnation qui se traduit alors par un allongement du cycle. Fréquence et intensité tendent à être en relation inverse[10]. Dès lors que le capital exalte les forces productives, son cycle se raccourcit et, inversement, les tendances à la stagnation favorisent l’allongement du cycle.
2.3 A la recherche d’une des bases matérielles du cycle des crises.
Après la crise tant attendue qui n'éclate qu'en 1857, Marx cherche un des fondements matériels du cycle des crises dans le temps de rotation du capital fixe[11].
« (...) A propos, peux-tu me dire en combien de temps vous renouvelez votre outillage, dans votre usine, par exemple? Babbage prétend qu'à Manchester en moyenne l'essentiel des machines est renouvelé tous les cinq ans. Cela me parait un peu surprenant et pas tout à fait plausible. Le laps de temps après lequel en moyenne les machines sont renouvelées est un élément important pour l'explication du cycle de plusieurs années que parcourt le mouvement industriel depuis que la grande industrie s'est imposée (...) » (Marx, Lettre à Engels 2/3/1858, Lettres sur le « Capital », Editions Sociales, p.87)
La réponse d'Engels lui paraît satisfaisante et suggère à Marx les commentaires suivants :
« Le chiffre de treize ans correspond, dans la mesure où on en a besoin, à la théorie: elle établit une unité pour une époque de reproduction industrielle qui coïncide plus ou moins avec la période de répétition des grandes crises ; naturellement le cycle de ces crises, en ce qui concerne l'intervalle, est déterminé par de tous autres éléments. Pour moi, l'important est de trouver dans les conditions matérielles immédiates de la grande industrie un élément de détermination de ces cycles ». (Marx, Lettre à Engels 5/3/1858, Lettres sur le « Capital », Editions Sociales, p.90)
Ces extraits nous montrent, outre le bon fonctionnement de la poste de cette époque, l'orientation théorique que Marx prend et qu'il conservera tout au long de son existence malgré certaines réserves d'Engels. Marx, en effet, revient sur le sujet en août 1862. Il s'intéresse à la différence entre la reproduction en valeur et la reproduction en nature du capital fixe.
« En tout cas, pendant ces douze ans, on ne doit pas remplacer chaque année en nature 1/12 des machines. Que fait-on de ce fond qui, annuellement, remplace 1/12 de l'outillage? N'est-ce pas, en fait un fonds d'accumulation destiné à élargir la production, abstraction faite de toute conversion de revenu en capital ? L'existence de ce fonds n'explique-t-elle pas en partie le taux très différent d'accumulation du capital chez les nations où la production capitaliste est développée, où par conséquent existe beaucoup de capital fixe par opposition aux nations où ce n'est pas le cas ? (...) » (Marx, Lettre à Engels 20/8/1862, Lettres sur le « Capital », Editions Sociales, p.128)
Engels qui a reçu peu de temps auparavant la fameuse lettre sur les prix de production et la rente absolue le dissuade de poursuivre une telle recherche:
« Il en est de même à propos de ton histoire d'usure des machines, à propos de laquelle toutefois, je crois fermement que tu t'es engagé sur une fausse piste. » (Engels, Lettre à Marx 9/9/1862, Lettres sur le « Capital », Editions Sociales, p.129)
Cinq ans plus tard, Marx repose le problème à son ami:
« Il y a de nombreuses années je t'avais écrit qu'un fonds d'accumulation, me semblait-il, se constituait, étant donné que le capitaliste emploie dans l'intervalle l'argent qui lui fait retour, avant de s'en servir pour remplacer le capital fixe. Tu t'es élevé contre cette conception dans une lettre d'une façon un peu superficielle. (...)
Toi, en tant que fabricant, tu dois bien savoir ce que vous faites des rentrées destinées au capital fixe avant le moment où il faut le remplacer en nature. Et tu dois me répondre sur ce point (pas en théorie, sur le plan purement pratique). » (Marx, Lettre à Engels 24/8/1867, Lettres sur le « Capital », Editions Sociales, p.175)
A cette époque, Marx se sentait assez fort dans ses convictions sur le cycle des crises pour écrire dans la seule partie du « Capital » publiée de son vivant, le livre I :
« Comme les corps célestes une fois lancés dans leurs orbes les décrivent pour un temps indéfini, de même la production sociale une fois jetée dans ce mouvement alternatif d'expansion et de contraction le répète par une nécessité mécanique (…) c'est de cette époque seulement [le mode de production capitaliste le plus moderne NDR] que datent les cycles renaissants dont les phases successives embrassent des années et qui aboutissent toujours à une crise générale, fin d'un cycle et point de départ d'un autre. Jusqu'ici la durée périodique de ces cycles est de dix ou onze ans, mais il n'y a aucune raison pour considérer ce chiffre comme constant. Au contraire on doit inférer des lois de la production capitaliste, telles que nous venons de les développer, qu'il est variable et que la période des cycles se raccourcira graduellement. » (Marx, Capital L.I, La Pléiade, T.2, p.1149-1150)
Si peu d'explications sont fournies par Marx (il n’en donnera jamais beaucoup d’autres) sur les relations entre le cycle des crises et la reproduction du capital fixe, il conservera ses certitudes jusque dans ses derniers manuscrits. Dans le livre II du « Capital », le dernier écrit des trois livres, qui contient également une analyse de la reproduction simple du capital fixe, que ne laisse apparaître aucune contradiction dans le procès de reproduction, Marx affirme cependant :
« On peut admettre que, pour les branches les plus importantes de la grande industrie, ce cycle de vie [du capital fixe NDR] est aujourd'hui de dix ans en moyenne. Nous nous abstenons cependant de donner ici un chiffre précis. Un point est acquis : ce cycle de rotations qui s'enchaînent et se prolongent pendant une série d'années, où le capital est prisonnier de son élément fixe, constitue une des bases matérielles des crises périodiques. Au cours du cycle, les affaires passent par des phases successives de dépression, d'animation moyenne, de précipitation, de crise. Les périodes d'investissement du capital sont certes fort différentes et fort discordantes; mais la crise constitue toujours le point de départ de nouveaux investissements importants. Elle fournit donc plus ou moins, si l'on considère la société dans son ensemble, une nouvelle base matérielle pour le prochain cycle de rotations. » (Marx, Capital L. II, La Pléiade T.2, p.614)
La question qui est posée à travers cette recherche ininterrompue et jamais complètement menée à son terme est la suivante : la reproduction du capital fixe contient-elle une contradiction qui puisse servir d'élément pour expliquer le cycle des crises ?
Si une telle contradiction avait un fondement matériel, il faudrait lui donner une expression mathématique. Ainsi serait démontré, que la reproduction du capital fixe contient un élément cyclique. Qui plus est, pour corroborer les perspectives de Marx, il faudrait démontrer que cet élément cyclique est en relation avec la période de rotation du capital fixe.
Le capital fixe contient également un autre facteur de crise que nous ne chercherons pas à développer ici. Il est lié à l’importance de la période de production du capital fixe. Pour produire et accumuler du capital fixe dont la période de production est importante (grands équipements, ouvrages d’art, etc.) un niveau élevé de la productivité du travail doit avoir été atteint. La possibilité comme la nécessité de trouver un exutoire afin de limiter la surproduction suppose, pour que ce type de production soit possible, l’existence d’une population qui puisse se libérer de la production immédiate. D’autre part, toutes choses égales par ailleurs, plus la période de production est importante plus le montant des avances en capital sera grand. Du temps va s’écouler entre le moment où un capital fixe de ce type est mis en chantier et le moment où il pourra être utilisé. Pendant toute cette période, le capital doit être avancé. Il permet d’immobiliser du capital dans la production d’un capital fixe qui n’aura qu’un effet ultérieur sur la productivité sociale et, de ce point de vue, joue un rôle pour limiter la surproduction. D’un autre côté, ces fortes avances de capital supposent un surplus relatif qui ne peut exister que sur la base d’une forte productivité du travail. Ce type de production est également un facteur permanent de crise. Ces crises ne sont pas des crises générales de surproduction mais des disproportions. Ces disproportions entre capital fixe et capital circulant du fait des variations qu’elles produisent dans la production du capital fixe (dont elles contribuent à augmenter la période de reproduction) jouent un rôle dans la périodicité du cycle[12]].
3. La divergence entre la masse et la valeur du capital fixe
3.1 La reproduction du capital fixe
Reprenons la question là où Marx l’a laissée. Les questions qu’il pose à Engels portent sur la différence entre le remplacement en nature du capital et la transmission de la valeur du capital fixe au produit. Le remplacement en nature d’un capital fixe intervient quand celui-ci ne peut plus fonctionner. Si son usure physique est la limite ultime de son utilisation, son usure « morale », son obsolescence, programmée ou non, est plus généralement à l’origine de son remplacement. Comme tout capital constant, le capital fixe ne fait que transmettre sa valeur au produit.
3.2 Exemple numérique
Admettons que dans la société existe, au temps t0, un capital fixe d'une valeur C0, de valeur 1000 représentant une masse M0 d’une valeur d’usage homogène quelconque, par exemple 1000 unités de machines d’un même type (nous ferons abstraction du caractère discret de la valeur d’usage).
Supposons que le temps de rotation du capital fixe soit égal à r, c’est-à-dire que le capital fixe transmet l’intégralité de sa valeur aux marchandises produites en r années. Dans notre exemple, nous posons r=2 années
Si, chaque année, le capital fixe est accumulé à un taux g (10% dans notre exemple), cela signifie que, dans notre cas particulier, la masse des machines accumulées sera de 1100, l’année suivante (t1).
D'un autre côté, comme nous posons une valeur unitaire, constante dans le temps, de chaque machine égale à 1, la masse des machines accumulée en t0-r était de :
![]()
Où M0 est la masse du capital fixe, le nombre de machines, au temps t0. Dans notre exemple, M0 = 1000 tandis que le taux d’accumulation du capital fixe est de g = 0,1 et la période de rotation r de deux ans (r=2)
Si nous appliquons ces données à l’équation ci-dessus, la masse du capital fixe, le nombre de machines, accumulées au temps t0-2, était de :
![]()
La valeur du capital fixe est transmise, via l’action du travail vivant, à la valeur des marchandises. La transmission de cette valeur se fait à chaque période de rotation au prorata de la durée de rotation du capital fixe (r - soit 2, dans notre exemple).
Au temps to où la valeur du capital fixe est 1000, la valeur transmise au produit marchandise sera donc de 500 car le temps de rotation du capital fixe est de deux ans. En d’autres termes, il transmet l’intégralité de sa valeur en deux ans. L’équation est donc (Mo v / r) où v est la valeur unitaire du capital fixe (1 dans notre exemple)
De même, la valeur transmise en t-1 et t0 par le capital fixe accumulé en t0-2 sera égale à :
![]()
Dans notre exemple, la valeur du capital fixe transmise au produit en t-1 et t0 est donc de 476,19 / 2 = 238,1.
Dans notre exemple, la masse actuelle (t0) du capital fixe est le résultat des deux dernières années d’accumulation du capital fixe puisque la période de rotation est de deux années. Nous avons calculé la masse du capital fixe accumulé en t-2, nous pouvons faire de même pour le capital accumulé en t-1. Nous savons que le taux d’accumulation du capital fixe est de g. Par conséquent, la masse du capital fixe accumulé en t-1 est égale à :
![]()
Comme la valeur unitaire de ce capital fixe est de 1, la valeur du capital fixe accumulé en t-1 sera également de 523,8.
La masse du capital fixe en t0 est le résultat de deux générations de capital fixe. Le capital fixe accumulé en t-2 et le capital fixe accumulé en t-1. La masse du capital fixe est donc égale à 476,2 + 523,8 soit 1000 unités de capital fixe. Il n’en va pas de même de la valeur de ce capital fixe. Celle-ci est égale à 476,2/2 + 523,8 soit 761,9 (la moitié de la valeur du capital fixe accumulé en t-2 a transmis sa valeur au produit en t-1).
Qu'advient-il avec l'accumulation du capital fixe lors de l'année t0 ?
Les machines accumulées lors de l'année t-2 deviennent hors d'usage, en même temps qu'elles achèvent de transmettre le reste de leur valeur au produit social. Par conséquent, 476,2 machines sont retirées de la production tandis que la valeur transmise au produit s'élève à 238,1. Pour obtenir l'intégralité de la valeur transmise au produit du fait de l’usure progressive du capital fixe, il faut ajouter celle fournie par les machines mises en place plus récemment qui demeurent encore en service mais dont la valeur diminue de moitié soit 523,8 / 2 = 261,9. La valeur totale du capital fixe qui est transmise au produit social lors de l'année t0 est donc égale à 238,1 + 261,9 = 500.
Si l’accumulation de capital fixe au taux de 10% se poursuit, la masse du nouveau capital fixe accumulé s’élèvera à 523,8 * 1,1 = 576,18. Comme la masse du capital fixe mise au rebut, la génération accumulée en t-2 se monte à 476,2, la masse totale du capital fixe passe de 1000 à 1100 (523,8 + 576,2 – 476,2). En revanche, la valeur nette du capital fixe accumulé est égale à 838,1 (576,2 + 261,9). La valeur nette du capital accumulé croît donc également de 10% ; la valeur nette du capital fixe a augmenté de 76,2, soit 10% de la valeur précédente du capital fixe (761,9). La valeur unitaire du capital fixe étant de 1, une valeur additionnelle de 76,2 ne permet d'augmenter la masse des machines que de 76,2 unités, alors que la masse requise pour une augmentation de 10% de la masse du capital fixe est de 10% de 1000, soit 100. C'est qu'il existe une divergence entre l'accroissement de la valeur du capital fixe et l’accroissement de sa masse. L'augmentation de la valeur résulte exclusivement de l'accumulation tandis que l'accroissement de la masse est réalisé non seulement par l'accumulation mais aussi par le jeu de la simple reproduction du capital fixe.
Nous avons vu que, en t0, la valeur du capital fixe transmise au produit se monte à 500. Cette valeur qui correspond à la reproduction simple du capital fixe permet l'achat de 500 unités de capital fixe, 500 machines, tandis que 476,2 seulement sont désormais hors d'usage. Il s'ensuit une augmentation de la masse du capital fixe de 23,8 (500 - 476,2) unités du simple fait de la reproduction simple du capital fixe. Si l'on ajoute à ces 23,8 unités provenant de la reproduction simple en valeur du capital fixe, les 76,2 fournies par l'accumulation, la masse totale des machines s'accroît de 100 (76,2 + 23,8) unités. De son côté, la valeur du capital fixe s'accroît de 10% soit 76,2 mais uniquement grâce à l'accumulation de la plus-value.
3.3 Formule générale
Dans notre exemple, c'est donc près de 24% (23,8/100) de l'augmentation de la masse du capital fixe qui est due à la simple reproduction de celui-ci. Quelle est la formule générale?
Sur la base de l'égalité entre l'unité de valeur d'usage et de valeur d'échange, en supposant que la valeur unitaire du capital fixe soit constante, la part due à la reproduction simple du capital fixe dans l’accroissement de sa masse est égale à:
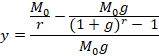
Nous pouvons simplifier l’équation en divisant chaque terme par M0g
![]()
Cette équation définit quelle part de l’accumulation de la masse du capital fixe est due à la simple reproduction de celui-ci du fait de la différence qui existe entre la valeur du capital fixe transmise au produit et la valeur de la masse du capital fixe définitivement détruite chaque année.
Dans notre exemple nous avons g=0,1 et r=2, donc
![]()
Si la période de rotation du capital fixe était de 3 pour un taux d’accumulation de 10% nous aurions le résultat suivant:
![]()
4. Les rapports masse valeur
4.1 L’évolution de la part de la reproduction simple : exemple numérique
Nous avons pu constater dans l’exemple précédent que la part dévolue à la simple reproduction du capital fixe jouait un rôle variable dans la masse du capital fixe accumulé.
Comment évolue cette part, pour un taux d’accumulation donné (g) quand la période de rotation du capital fixe (r) varie ?
Nous avons obtenu l’équation suivante :
![]()
Par exemple avec g = 20% nous obtenons le tableau suivant :
|
g |
r |
y |
|
20% |
2 |
22,7% |
|
20% |
3 |
29,3% |
|
20% |
4 |
31,8% |
|
20% |
5 |
32,8% |
|
20% |
6 |
32,9% |
|
20% |
7 |
32,7% |
|
20% |
8 |
32,2% |
|
20% |
9 |
31,5% |
|
20% |
10 |
30,7% |
A partir des données calculées nous pouvons tracer la courbe suivante :
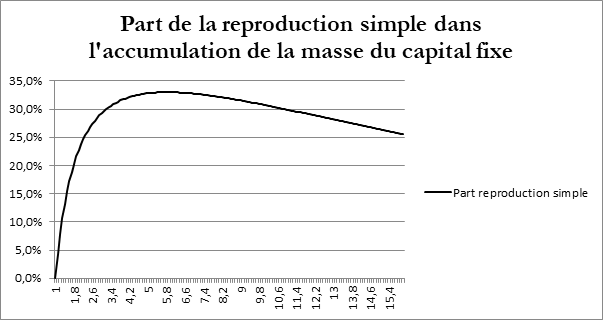
Dans cet exemple, où le taux d’accumulation du capital fixe est de 20%, la courbe passe par un maximum quand le temps de rotation du capital fixe est d’environ 6 ans. A ce moment, la part de la reproduction simple du capital fixe représente environ le tiers de l’accumulation de la masse du capital fixe.
4.2 L’équation générale
Le maximum de la courbe correspond, mathématiquement, au point où la dérivée de la courbe est nulle.
Il s’agit donc de déterminer la dérivée de l’équation
![]()
Nous savons que r est optimum pour un g donné quand la dérivée y’ de cette équation est nulle.
A quoi est égale cette dérivée ?
La dérivée d’une différence est égale à la différence de ses dérivées.
Donc,
la dérivée de y soit y’ est égale à la dérivée de ![]() moins la dérivée de
1/((1 + g)r – 1)
moins la dérivée de
1/((1 + g)r – 1)
La
dérivée de ![]() est égale à
est égale à ![]() (la dérivée d’une fonction de type 1/u
est égale à -u’/u2 et comme g est donné, il est traité comme une
constante – la dérivée d’une constante est nulle -)
(la dérivée d’une fonction de type 1/u
est égale à -u’/u2 et comme g est donné, il est traité comme une
constante – la dérivée d’une constante est nulle -)
Le deuxième terme est également du type 1/u et donc la dérivée est égale à –u’/u2
Ici
u = ![]()
La
dérivée u’ de u est la plus complexe. Elle se décompose en deux membres qui
forment une différence. Soit ![]() et 1. 1 est une constante et donc sa
dérivée est nulle. Il reste à calculer la dérivée de
et 1. 1 est une constante et donc sa
dérivée est nulle. Il reste à calculer la dérivée de ![]() qui est une fonction exponentielle de
base
qui est une fonction exponentielle de
base ![]() .
.
Ce
type de fonction ![]() a une dérivée égale à
a une dérivée égale à ![]()
Par
conséquent la dérivée u’ est égale à ![]()
La dérivée du deuxième terme est donc :
![]()
La dérivée de l’équation est donc :
![]()
Quand la dérivée est nulle, r est maximum.
Donc r est maximum quand
![]()
La transformation de l’équation précédente donne :
![]()
Puis
![]()
4.3 Le maximum du rapport entre taux d’accumulation et la période de rotation du capital fixe
Lorsque g tend vers 0, la part maximum de la reproduction simple dans l’accumulation de la masse du capital fixe est obtenue pour une valeur de r toujours plus grande.
Par exemple quand g vaut 5%, la dérivée est nulle quand r vaut environ 11 ans contre 6 ans environ lorsque g est égal à 20%.
Le tableau ci-dessous détaille, pour une valeur de g donnée, quelle valeur de r annule la dérivée et donc permet d’obtenir un maximum de la part de la reproduction simple dans l’accumulation de la masse du capital fixe.
|
g |
r |
|
0,5% |
34,7 |
|
1% |
24,5 |
|
1,5% |
20,1 |
|
2% |
17,4 |
|
2,5% |
15,6 |
|
3% |
14,3 |
|
3,5% |
13,2 |
|
4% |
12,4 |
|
4,5% |
11,7 |
|
5% |
11,1 |
|
5,5% |
10,6 |
|
6% |
10,2 |
|
6,5% |
9,8 |
|
7% |
9,4 |
|
7,5% |
9,1 |
|
8% |
8,8 |
|
8,5% |
8,6 |
|
9% |
8,4 |
|
9,5% |
8,2 |
|
10% |
8,0 |
|
11% |
7,6 |
|
12% |
7,3 |
|
13% |
7,1 |
|
14% |
6,8 |
|
15% |
6,6 |
|
16% |
6,4 |
|
17% |
6,2 |
|
18% |
6,1 |
|
19% |
5,9 |
|
20% |
5,8 |
|
25% |
5,3 |
|
30% |
4,9 |
|
40% |
4,3 |
|
50% |
4,0 |
A partir de ces données, nous pouvons établir la courbe suivante. Elle relie le maximum de la période de rotation à un taux d’accumulation du capital fixe donné.
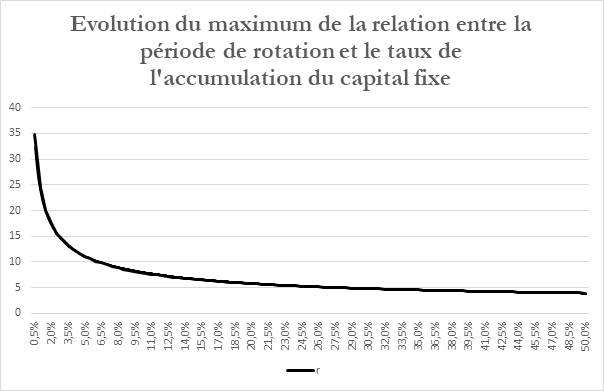
4.4 Evolution de la part maximum de la reproduction simple dans le taux de l’accumulation de la masse du capital fixe
Dans le chapitre 24.1, nous avons montré, en faisant varier le temps de rotation du capital fixe (r), comment évoluait la part de la reproduction simple pour un taux de l’accumulation (g) de la masse du capital fixe donné.
A partir des résultats du chapitre 24.2, nous pouvons déterminer la part maximum que représente la reproduction simple du capital fixe dans le processus de reproduction élargie de la masse du capital fixe.
L’équation de départ était :
![]()
Comment évolue cette équation pour le r maximum des divers taux de croissance ?
En remplaçant, dans l’équation ci-dessus, g et r par les valeurs obtenues lors du calcul des maxima, nous obtenons le tableau et la courbe suivants :
|
g |
r |
Part reproduction simple |
|
0,5% |
34,7 |
47,1% |
|
1% |
24,5 |
45,9% |
|
1,5% |
20,1 |
45,0% |
|
2% |
17,4 |
44,3% |
|
2,5% |
15,6 |
43,6% |
|
3% |
14,3 |
43,0% |
|
3,5% |
13,2 |
42,5% |
|
4% |
12,4 |
42,0% |
|
4,5% |
11,7 |
41,5% |
|
5% |
11,1 |
41,0% |
|
5,5% |
10,6 |
40,6% |
|
6% |
10,2 |
40,2% |
|
6,5% |
9,8 |
39,8% |
|
7% |
9,4 |
39,5% |
|
7,5% |
9,1 |
39,1% |
|
8% |
8,8 |
38,8% |
|
8,5% |
8,6 |
38,5% |
|
9% |
8,4 |
38,2% |
|
9,5% |
8,2 |
37,8% |
|
10% |
8,0 |
37,6% |
|
11% |
7,6 |
37,0% |
|
12% |
7,3 |
36,5% |
|
13% |
7,1 |
36,0% |
|
14% |
6,8 |
35,5% |
|
15% |
6,6 |
35,0% |
|
16% |
6,4 |
34,6% |
|
17% |
6,2 |
34,2% |
|
18% |
6,1 |
33,8% |
|
19% |
5,9 |
33,4% |
|
20% |
5,8 |
33,0% |
|
25% |
5,3 |
31,3% |
|
30% |
4,9 |
29,8% |
|
40% |
4,3 |
27,4% |
|
50% |
4,0 |
25,4% |
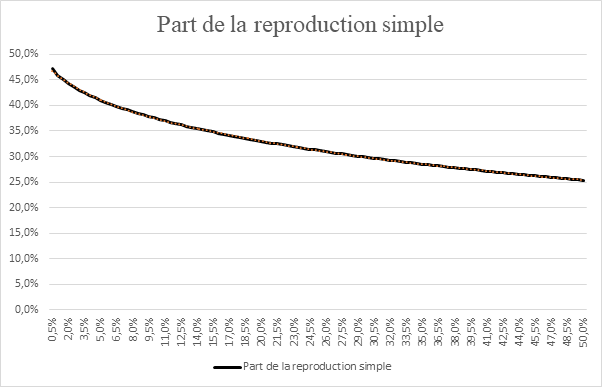
Par conséquent, pour le "r" maximum d'un "g" donné, la part de l’accumulation de la masse du capital fixe qui résulte de sa reproduction simple va en diminuant avec l'élévation du taux de l’accumulation. Par exemple, cette part passe de plus de 47% de l’augmentation de la masse du capital fixe, pour un taux de 0,5%, à moins de 33% quand le taux de l’accumulation est de 20%.
Si nous limitons le domaine de définition des courbes étudiées à des bornes compatibles avec la réalité économique générale, il reste que la reproduction simple du capital fixe joue un très grand rôle dans l'accumulation globale.
Le taux de l’accumulation du capital fixe, dépend, d’une part, du taux de profit et, d’autre part, du taux d’accumulation de la plus-value. La tendance à la baisse du taux de profit induirait plutôt une baisse du taux de l’accumulation du capital fixe. Mais cette tendance est contrebalancée par le fait que le capital fixe représente une part croissante du produit social. Baisse du taux de profit et accroissement du taux de l’accumulation du capital fixe ne sont donc pas, jusqu’à un certain point, incompatibles.
Quand le taux de l’accumulation du capital fixe (g) diminue, le maximum du temps de rotation du capital fixe (r) s'élève. Avec le développement du progrès technique et de la dévalorisation du capital qui l’accompagne (que ce soit du fait de la hausse de la productivité pour reproduire ce capital fixe ou du fait de son obsolescence) on devrait s’attendre à ce que le cours de la production capitaliste s’accompagne d’un raccourcissement du temps de rotation.
À supposer qu’une part élevée de l’accumulation de la masse du capital fixe due à la reproduction simple soit un avantage pour la production capitaliste, notamment en lui conférant une plus grande stabilité, ce n’est que si g et r vont en sens inverse l’un de l’autre que cet optimum serait atteint. L'obtention de l'optimum pour un taux de croissance donné serait donc toujours plus difficile à mesure que le mode de production capitaliste avance.
En même temps, les fluctuations du taux de l’accumulation du capital fixe sont suffisamment importantes pour que celui-ci ne soit jamais, sinon par hasard, en relation avec la période de rotation optimale correspondante. Nous inférons que la stabilité du temps de rotation du capital fixe est plus grande que celle du taux de l’accumulation du capital fixe. D’autre part, même pour de grands écarts de taux, la part de la reproduction simple reste très élevée. Enfin, la plage de valeur, autour du maximum, est suffisamment ample[13] pour que nous ne puissions en conclure que les effets d’une divergence entre les mouvements, jugés favorables, de g et r soient de faible portée.
5. L'élément cyclique de la reproduction simple
5.1 Exemple numérique
Dans les chapitres précédents, nous avons mis en relief une particularité de la reproduction élargie du capital fixe en montrant l’importance du rôle de la reproduction simple dans l’accumulation de la masse du capital fixe. La divergence entre la valeur du capital fixe transmise au produit social et son remplacement en nature peut-elle contenir un élément cyclique ?
Pour avoir un élément de réponse à cette question, supposons que l'accumulation de capital fixe due à l'accumulation de la plus-value s'arrête. Comment évoluent, dans ce cas, la masse et la valeur du capital fixe ?
Prenons l'exemple suivant : l’accumulation du capital fixe a connu un taux de 20% pour une durée de la période de rotation du capital fixe égale à six années, ce qui, nous l'avons vu, constitue, à peu près, un couple optimum.
Supposons une masse de capital fixe de 1000 unités dont la valeur totale est de 1000. Cette masse se décompose, suivant la date à laquelle le capital a été accumulé, en 100,7 unités accumulées en t‑6, 120,85 en t-5, 145,01 en t-4, 174,02 en t-3, 208,82 en t-2 et 250,59 en t-1. Dorénavant, comme il n'y a plus d'accumulation de la plus-value, seule joue la reproduction simple du capital fixe.
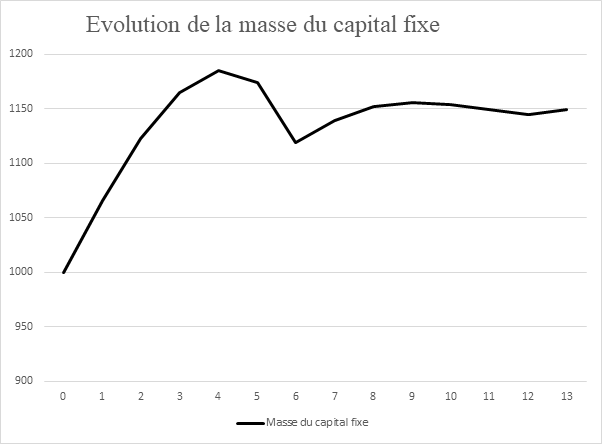
Au temps t0, 100,7 unités de capital fixe sont définitivement usées, tandis que le renouvellement du capital fixe permet un accroissement de la masse du capital fixe de 166,7 (1000/6) puisque la valeur transférée au produit est de 1000 / 6. Ainsi, tandis que la valeur du capital fixe se maintient à 670,2, la masse du capital fixe s'élève en t1 à 1066. Le même processus se poursuit en t2 pour atteindre un maximum en t4, comme on peut le voir sur le tableau et la courbe qui en est issue, ci-dessous: